AC 自动机
字典树(Tire 树)
Trie 树是一种多叉树的结构,每个节点保存一个字符,一条路径表示一个字符串。
下图表示了字符串: him 、 her 、 cat 、 no 、 nova 构成的 Trie 树。
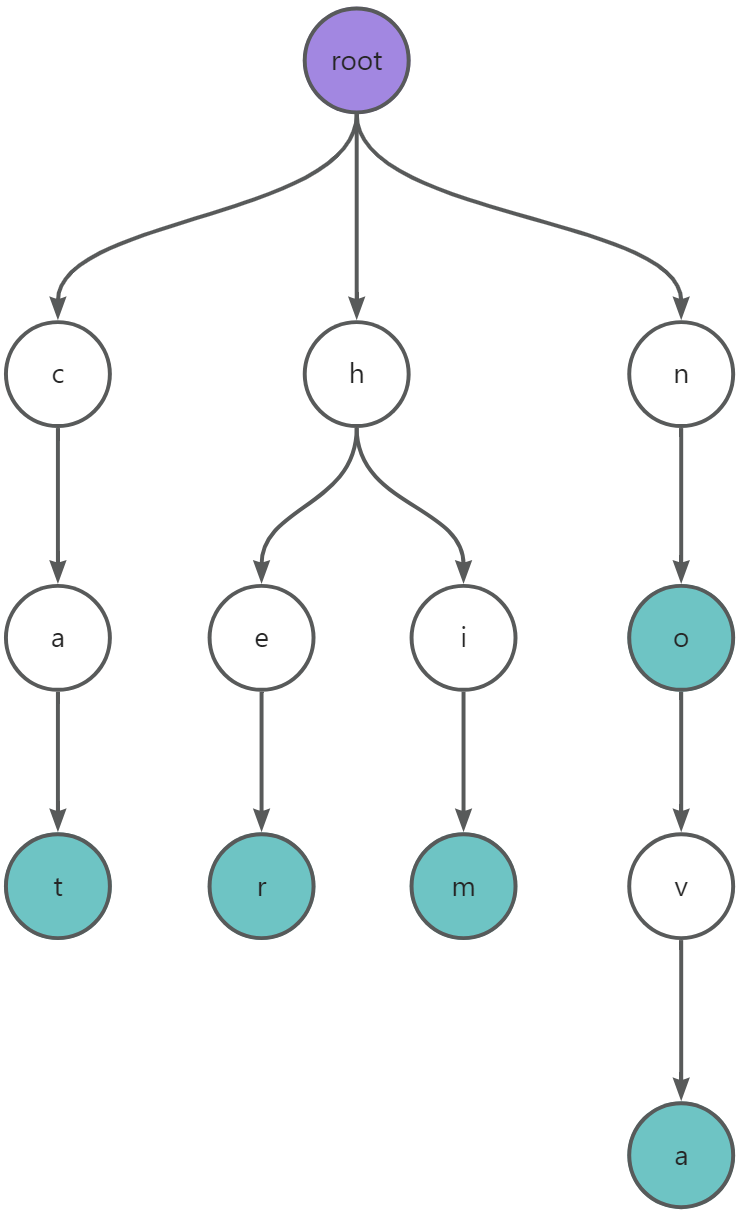
从图中可以看出 Trie 树包含以下性质:
根节点不包含字符,其他节点包含一个字符。
从根节点到某一节点经过的字符连接起来构成一个字符串。如图中的
him、her、cat、no、nova。一个字符串与 Trie 树中的一条路径对应。
在实现过程中,会在叶节点中设置一个标志,用来表示该节点是否是一个字符串的结尾,本例中用青色填充进行标记。
如何构建 Tire 树
Trie 树中每个节点存储一个字符,从根节点到叶节点的一条路径存储一个字符串。另外,有公共前缀的字符串,他们的公共前缀会共用节点。如 her、 him 共用 h 节点。

根节点不存在子节点 h,因此创建子节点 h。
在节点
h的基础上插入第二个字符i。节点
h不存在子节点i,创建子节点i。在节点
i的基础上插入第三个字符m。节点
i不存在子节点m,创建子节点m。并将该节点标记为字符串结束标志,完成him字符串插入。
插入 her :
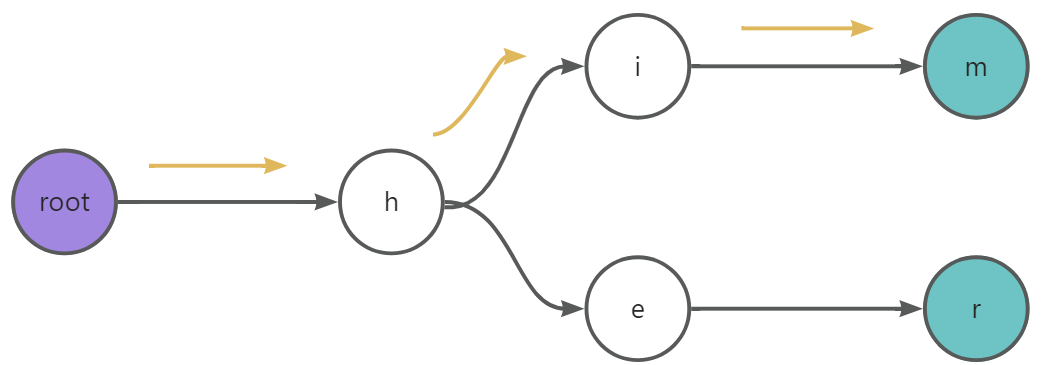
Trie 树有什么用?
Trie 树又叫字典树。字典是用来查字的,Trie 树最基本的作用是在树上查找字符串。
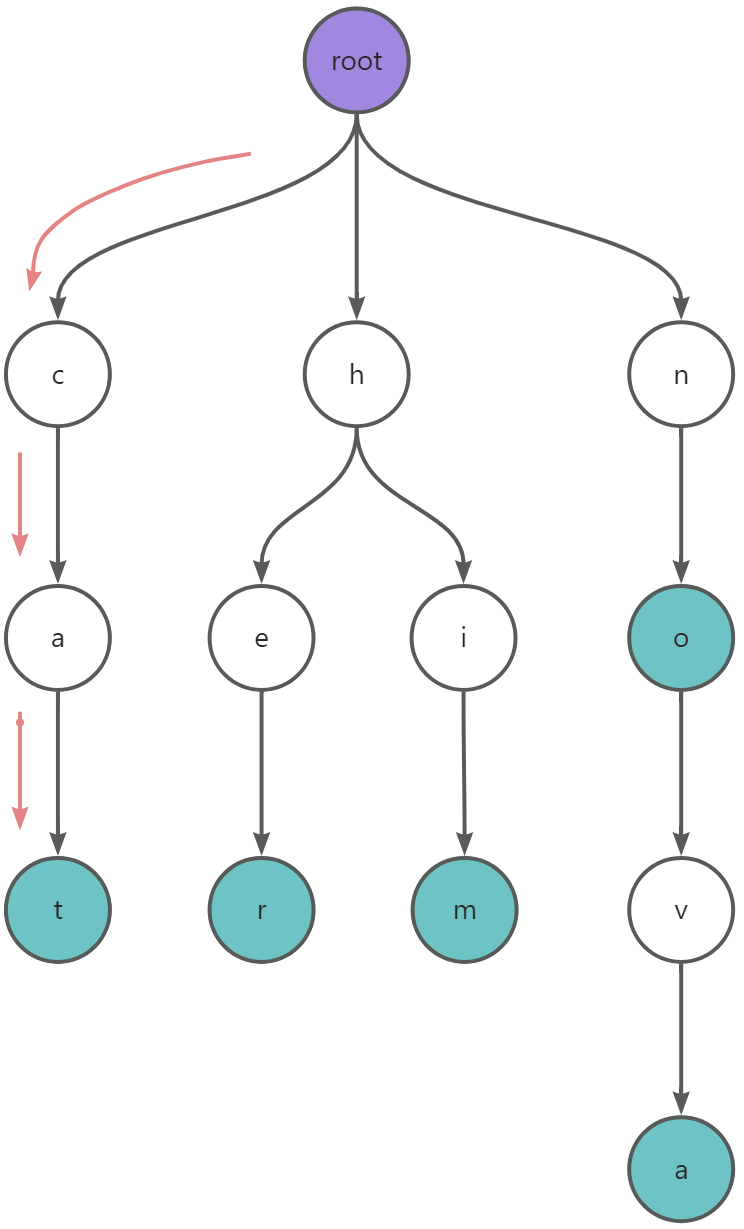
例如有 5 个字符串: him 、 her 、 cat 、 no 、 nova 。现在要查找 catch 是否存在。
如果使用暴力的方法,需要用 catch 与这 5 个字符串分别进行匹配,效率较低。
如果将这 5 个字符串存储成 Trie 的结构,只需要顺着路径依次比较,比较完 cat 之后,没有节点与 c 匹配,所以字符串集合中不存在 catch。
字典树与 DFA
字典树(Trie)是一种很特别的树状信息检索数据结构。利用字符串的公共前缀(common-prefix)来减少查询时间,搜索时间为 O(d),d 为树的深度。
字典树的原则:
根节点不含字符
根节点到某一终点连起来即为搜索字符串
任意节点的所有子节点包含字符不同
字典树的查找方法也很简单:
每次从根结点开始搜索;
获取关键词的第一个字符,根据该字符选择对应的子节点,转到该子节点继续检索;
在相应的子节点上,获取关键词的第二个字符,进一步选择对应的子节点进行检索;
以此类推,进行迭代过程;
在某个节点处,关键词的所有字母已被取出,则读取附在该节点上的信息,查找完成
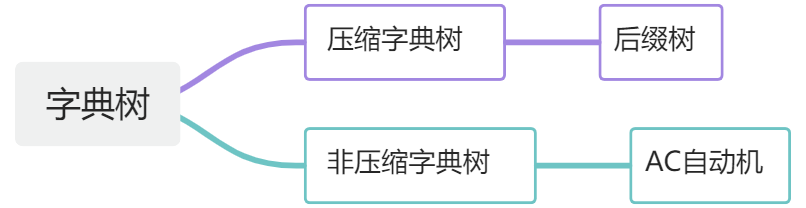
而字典树又分为压缩字典树、非压缩字典树等,我们的 AC 自动机算法就是一棵典型的非压缩字典树。
AC 自动机是一种典型的前缀搜索算法:
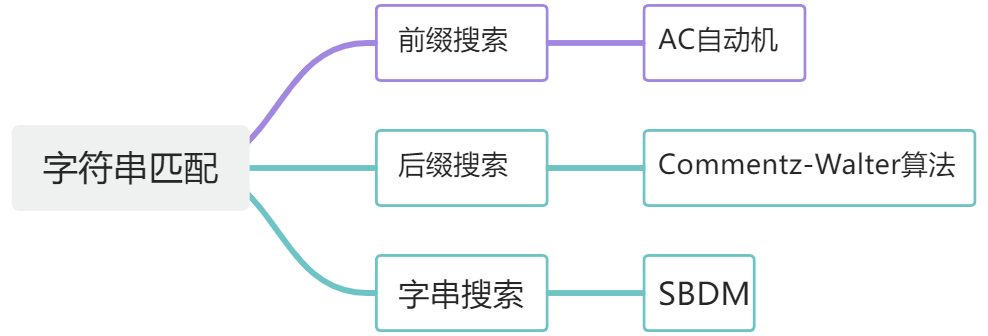
什么是确定有限自动机 (Deterministic Finite Automaton, DFA)呢?
自动机(Automaton):就是一个代码块,只做一件事——接收输入值,和状态值,输出同为状态值的结果。
有限(Finite):是指自动机接收、输入的状态种类是有限的。不然就是英菲尼迪了
确定(Deterministic):是指自动机的输出状态是单一的一个状态,不然就是 NFA 了。
典型的 DFA
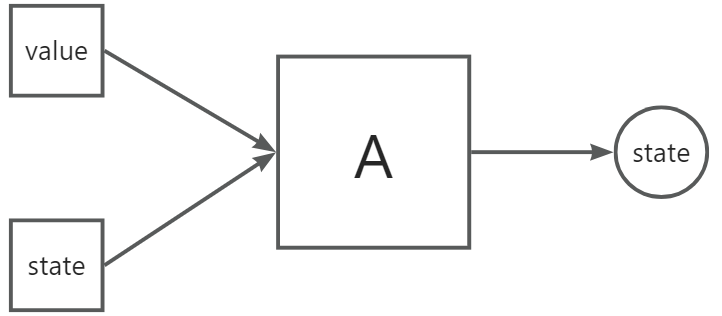
典型的 NFA
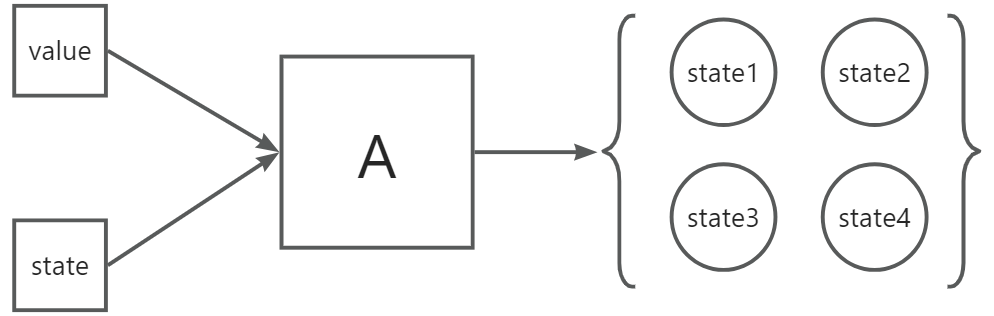
DFA与字典树有什么不同
DFA(Deterministic Finite Automaton)是用来识别、验证或识别输入是否属于某种语言的抽象数学模型,而字典树(Trie)是一种树形数据结构,通常用于快速检索大量的字符串数据集合。在实际应用中,DFA 通常用于字符串匹配和识别,而字典树用于实现高效的字符串检索和前缀匹配。
AC 自动机
AC 自动机(Aho-Corasick automaton)算法于 1975 年产生于贝尔实验室,是一种用于解决多模式匹配问题的经典算法。常被用来做敏感词检测,后处理的替换模块也是基于此。
值得注意的是,AC 自动机应当属于基于前缀搜索的非压缩字典树
特点:
基于非压缩字典树(trie)
多模式匹配,速度快且稳的一批
基于确定有限自动机(DFA)
UNIX 之中的 grep 就是用的该算法实现的。
AC 自动机原理
以模式串(替换列表)为 his、hers、she 为例,首先构建一个 trie:
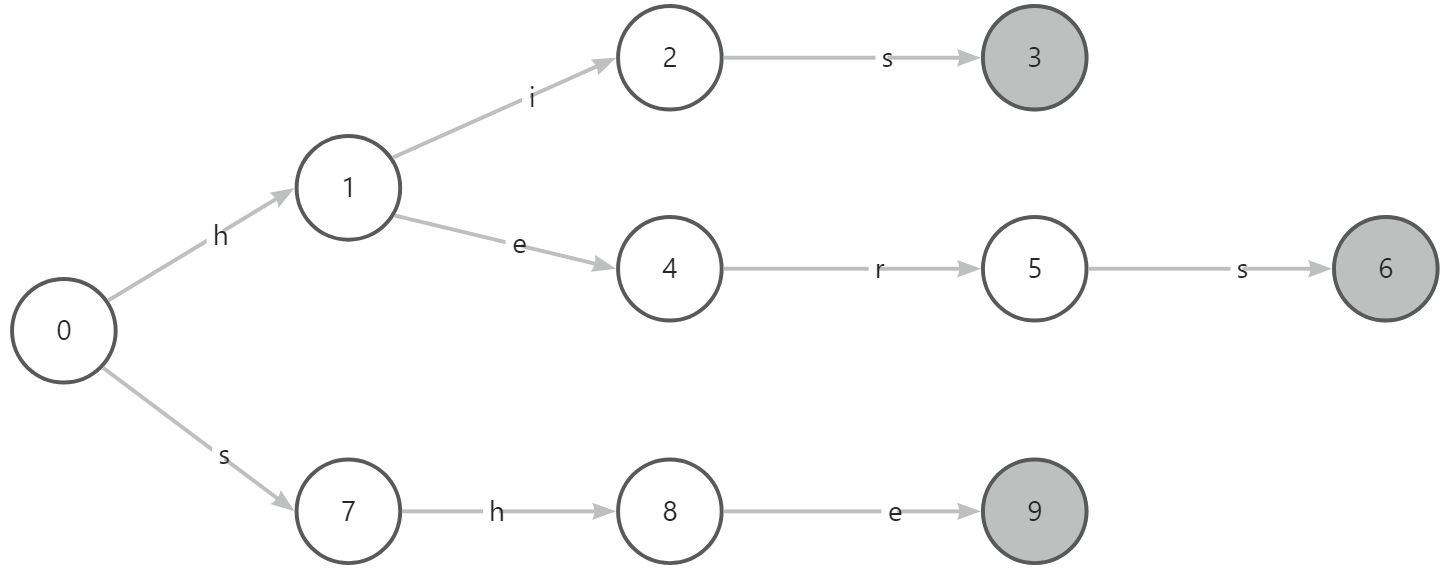
这时,我们就需要“失配指针”来帮忙了,为了节省匹配次数,不放弃已匹配过的部分,AC 自动机之中加入了 fail 路径,又叫失配路径(指针)。失配指针能够在节点无法匹配下个字符的时候,转向其他节点。
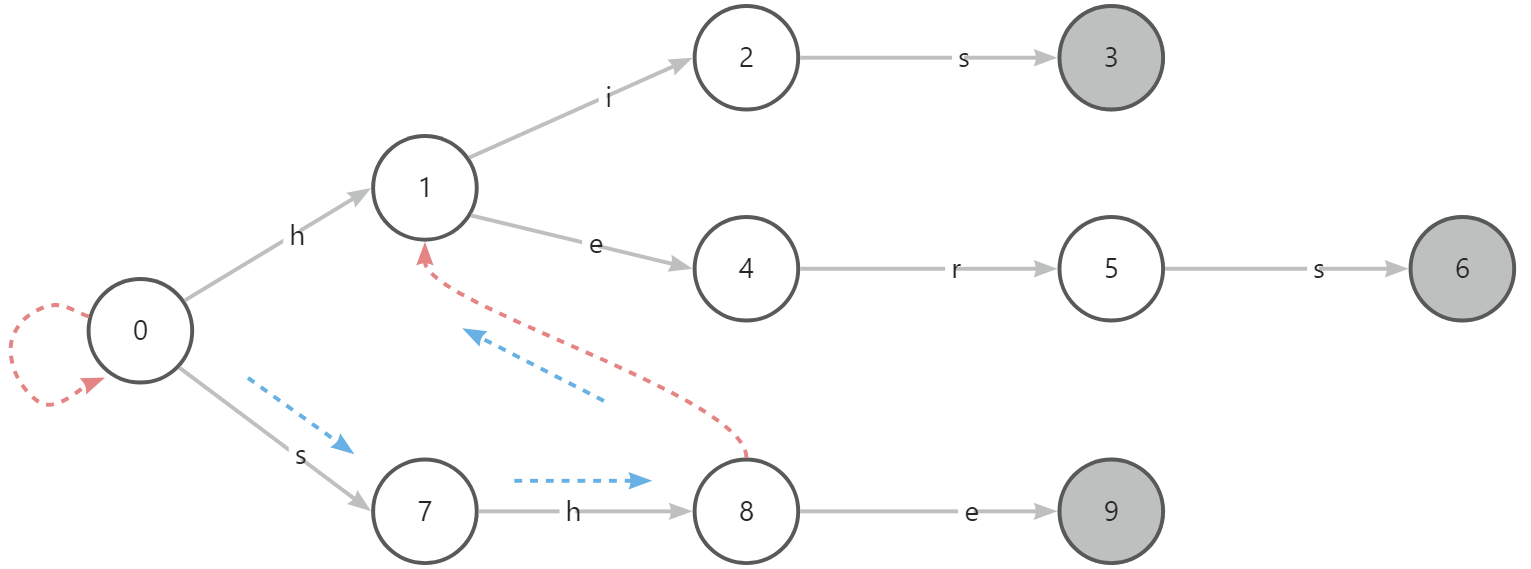
那失配指针是如何构建的呢?
对于 AC 自动机的根节点的子节点,将它们的失配指针设为根节点。
对于根节点的子节点,设置它们的失配指针为根节点,并将它们加入到队列中。
依次处理队列中的节点,对于每个节点,将其子节点的失配指针设置为该节点的失配指针指向的节点的相应子节点,如果找不到则继续向上查找。
重复上述步骤,直到处理完所有节点为止。
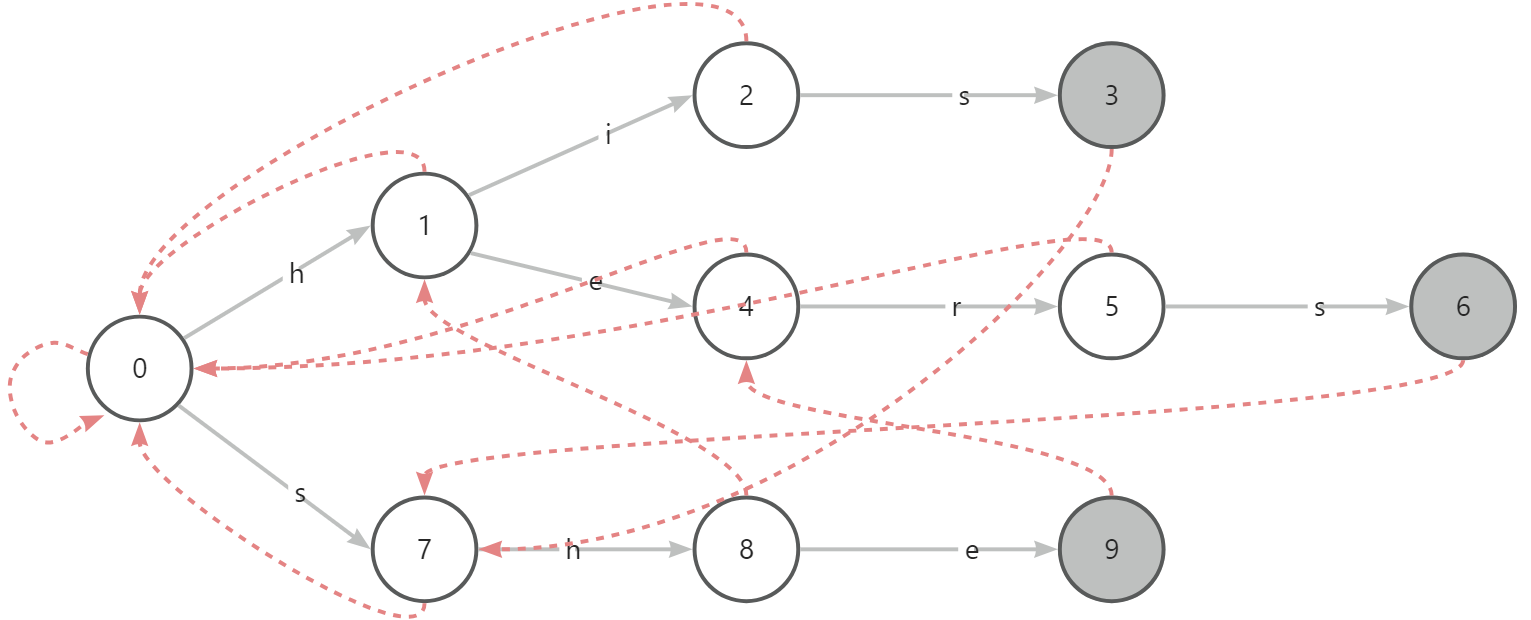
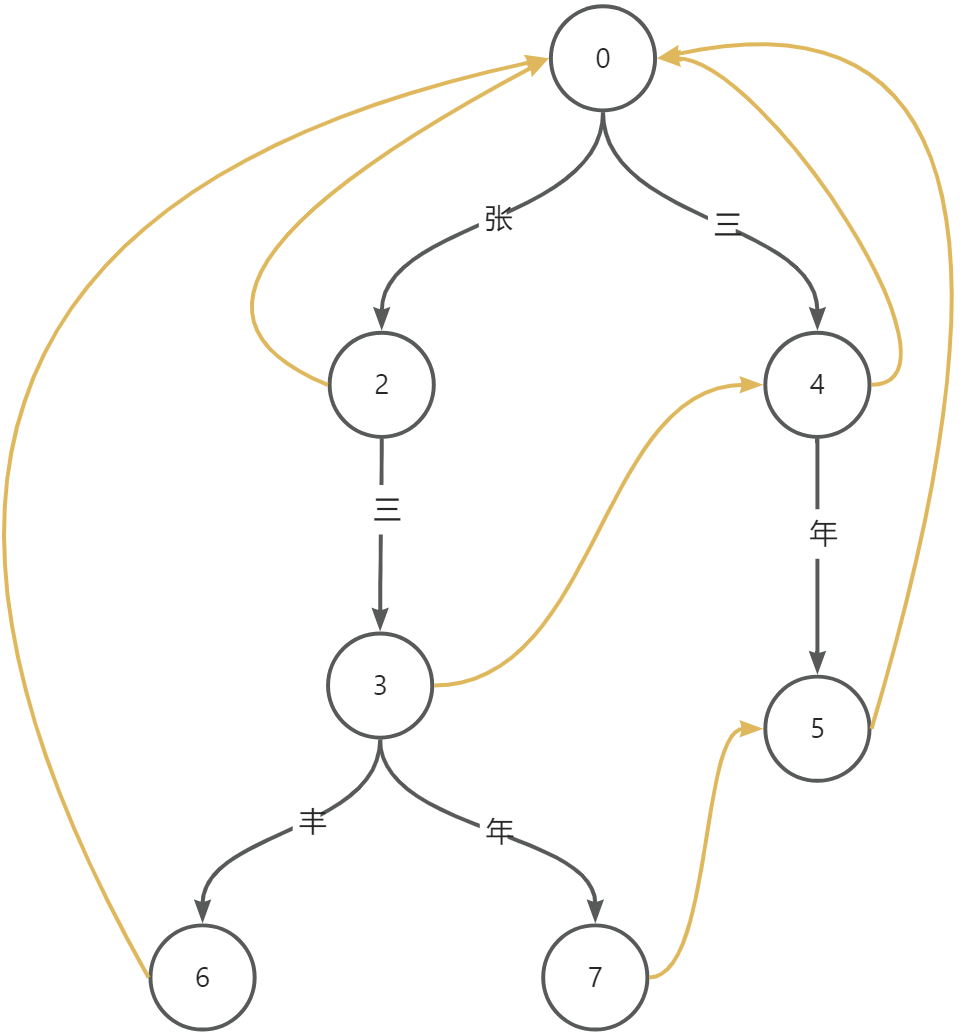
代码示例
class ACNode {
public char data;
public Map<Integer, ACNode> children = new HashMap<>();
public boolean isEndingChar = false;
public int length = -1;
public ACNode fail;
public ACNode(char data) {
this.data = data;
}
}
public class ACAutomaton {
private final ACNode root;
public ACAutomaton() {
root = new ACNode('/');
}
/**
* 通过遍历关键字的字符并根据需要创建新节点,将关键字插入到trie树中。
*/
public void insert(String text) {
ACNode p = root;
for (int i = 0; i < text.length(); i++) {
char ch = text.charAt(i);
if (!p.children.containsKey((int) ch)) {
ACNode newNode = new ACNode(ch);
p.children.put((int) ch, newNode);
}
p = p.children.get((int) ch);
}
p.isEndingChar = true;
p.length = text.length();
}
/**
* 为trie中的每个节点构造失败指针。当输入文本中的字符与当前节点的任何子节点不匹配时,这些指针用于有效地回溯。
*/
public void buildFailurePointer() {
Queue<ACNode> queue = new LinkedList<>();
root.fail = null;
queue.add(root);
while (!queue.isEmpty()) {
ACNode p = queue.remove();
for (ACNode pc : p.children.values()) {
if (p == root) {
pc.fail = root;
} else {
ACNode q = p.fail;
while (q != null) {
ACNode qc = q.children.get((int) pc.data);
if (qc != null) {
pc.fail = qc;
break;
}
q = q.fail;
}
if (q == null) {
pc.fail = root;
}
}
queue.add(pc);
}
}
}
/**
* 匹配
*/
public List<String> match(String text) {
List<String> ret = new ArrayList<>();
ACNode p = root;
for (int i = 0; i < text.length(); i++) {
char ch = text.charAt(i);
while (!p.children.containsKey((int) ch) && p != root) {
p = p.fail;
}
p = p.children.getOrDefault((int) ch, root);
ACNode tmp = p;
while (tmp != root) {
if (tmp.isEndingChar) {
ret.add(text.substring(i - tmp.length + 1, i + 1));
}
tmp = tmp.fail;
}
}
return ret;
}
public static void main(String[] args) {
ACAutomaton ac = new ACAutomaton();
ac.insert("张三");
ac.insert("三年");
ac.insert("张三年");
ac.insert("张三丰");
ac.buildFailurePointer();
List<String> ret = ac.match("张三年");
System.out.println(ret);
}
}运行结果:
[张三,张三年,三年]